Wie man das Schwarze Loch im Milchstraßenzentrum sichtbar macht

Heino Falcke
Sterne und Weltraum, 1/2000, S. 12

Von ihrer Existenz sind die meisten Astophysiker inzwischen überzeugt, aber wirklich gesehen hat sie noch niemand: Schwarze Löcher. Doch es scheint, als ob sich dies in absehbarer Zeit ändern könnte. Das notwendige Schwarze Loch liegt dabei direkt vor unserer kosmischen Haustür, im Zentrum unserer Milchstraße, und die entsprechenden Techniken zur Beobachtung des Loches werden zur Zeit von Radioastronomen entwickelt.

Wie kann man nun ein Schwarzes Loch sehen? Die besondere Eigenschaft schwarzer Löcher ist ja, dass sie den Raum um sie herum so stark krümmen, das selbst Licht nicht mehr zu einem entfernten Beobachter auf der Erde gelangen kann, sondern zum Schwarzen Loch hin abgelenkt wird. Der Punkt ohne Wiederkehr für Photonen ist dabei der »Ereignishorizont« - bei maximal rotierenden Schwarzen Löchern gegeben durch das Produkt aus Gravitationskonstante und Masse, geteilt durch die Lichtgeschwindigkeit im Quadrat (R_g=GM/c²). Alles was sich hinter dem Ereignishorizont abspielt entzieht sich unserer direkten Beobachtung. Ursache dieses Phänomens ist eine extrem hohe Massenkonzentration auf sehr kleinem Raum - die Masse der Erde auf einen Zentimeter Durchmesser konzentriert würde z.B. ein solches Schwarzes Loch ergeben.

Die große Masse Schwarzer Löcher führt nicht nur dazu, dass Licht abgelenkt wird, sondern sie zwingt auch Gas und Staub in ihrer Umgebung auf Spiralbahnen die letztendlich im Ereignishorizont enden. Der größte Teil der einfallenden Masse und Energie verschwindet dann für immer von der kosmischen Bildfläche und nur einem kleinen Teil gelingt es zu entkommen, z.B. in Form von sogenannten Radiojets wie sie inzwischen in vielen Schwarz-Loch-Kandidaten gesehen werden.

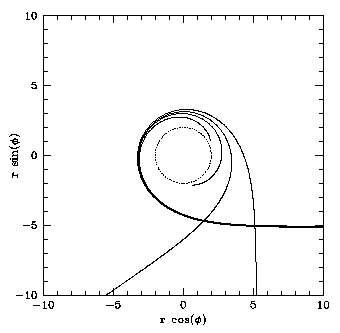
Das Einströmen in den Ereignishorizont wie auch das Entweichen der Radiojets passiert nicht lautlos, sondern die ein- und ausströmende Materie macht durch mehr oder weniger starke Emission von Photonen verschiedener Energie - vom Radio- bis zum Röntgenbereich - auf sich aufmerksam. Theoretisch sollten Photonen sogar in der direkten Nähe des Ereignishorizonts abgestrahlt werden, allerdings: je näher ein Photon am Schwarzen Loch abgestrahlt wird, desto größer ist die Wahrscheinlichkeit das es im Ereignishorizont verschwindet. Diese Wahrscheinlichkeit nimmt drastisch zu, sobald ein Photon innerhalb des »Photonenorbits« entsteht. Der Photonenorbit ist eine theoretische Bahn, auf dem Licht unendlich oft um das Schwarze Loch kreisen kann (z.B. Bardeen 1973). In der Realität bedeutet dies, dass Photonen, die sich auf Tangentialbahnen innerhalb des Photonenorbits befinden früher oder später in das Loch hinein fallen, während Photonen auf weiteren Bahnen entkommen und entdeckt werden können (siehe Bild 1).

Bild1: Photonenbahnen in der Nähe eines schwarzen Lochs. Die Bahnen von vier Photonen mit fast identischem Ursprung, die ein Schwarzes Loch tangential streifen (Einfall von rechts), werden in der Nähe des Photonenorbits sehr unterschiedlich abgelenkt. Die zwei inneren Photonen enden letztlich im Ereignishorizont (gestrichelter Kreis), während die äußeren beiden Photonen zu einem Beobachter im Unendlichen entkommen. Ein Photon dazwischen könnte theoretisch ewig um das Schwarze Loch kreisen.

Das schlagartige Verschwinden von Photonen sollte sich dann auch auf die visuelle Erscheinung eines Schwarzen Lochs auswirken. Eingebettet in einen leuchtenden Halo von aus- oder einfallendem Gas würde man dann das Schwarze Loch als einen »Schatten« erblicken (Falcke, Melia, Agol 2000; de Vries 2000).

In der Tat kann man solche Bilder auf dem Computer simulieren. Wenn man die Masse und die Rotation des Schwarzen Lochs vorgibt, ist die Bahn eines Photons von jedem Ort aus durch Einsteins allgemeine Relativitätstheorie festgelegt und kann berechnet werden. Durch ein sogenanntes Ray-Tracing-Verfahren, bei dem Lichtbahnen bis zum Beobachter verfolgt werden, entsteht dann im Computer ein vollständiges, virtuelles Bild der Umgebung eines Schwarzen Lochs.

Ein Beispiel für eine solche Rechnung wird in der linken Spalte von Bild 2 gezeigt. Man sieht deutlich den klaren, kreisförmigen Schatten im Zentrum der Emission. Dieser Schatten ist immer vorhanden, solange das Emissionsgebiet transparent (»optisch dünn«) ist. Die Position des Schattens ändert sich nur ein wenig zwischen einem rotierendem und einem nicht-rotierenden Schwarzen Loch und auch der Durchmesser ist nur wenig von der Rotation des Schwarzen Lochs abhängig - entscheidend ist hingegen die Masse. Als Faustformel kann man rechnen, dass der Schatten ungefähr einen Durchmesser von 10 mal dem Gravitationsradius, also R_Schatten~10 GM/c² hat. Der Schatten ist deutlich größer als der Ereignishorizont weil, unter anderem, das Schwarze Loch als seine eigene Gravitationslinse funktioniert und so sein Bild vergrößert.

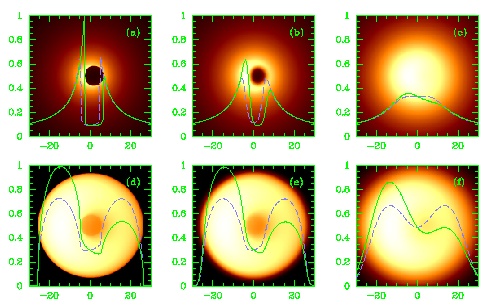
Bild2: Computersimulation eines in transparentes, leuchtendes Gas eingehülltes Schwarzen Lochs. Die horizontale Achsenmarkierung gibt die räumliche Skala in Einheiten des Gravitationsradius (R_g) an, während die vertikale Skala relative Intensitätswerte für vertikale (gestrichelte Linie) und horizontale (durchgezogene Linie) Querschnitte durch das Bild angibt. Die obere Reihe ist für ein rotierendes und die untere Reihe für ein nicht-rotierendes Schwarzes Loch. Die mittlere und rechte Spalte zeigen Bilder, wie man sie mit Radiointerferometern (VLBI) bei 0.6 und 1.3mm Wellenlänge für das Schwarze Loch im Zentrum der Milchstraße erwarten würde. Der Schatten ist immer noch klar sichtbar. Erste experimentelle Beobachtungen bei 1.4mm Wellenlänge hat es schon gegeben.

Der Durchmesser des Schattens wächst linear mit der Masse und die beobachtbare Größe am Himmel schrumpft linear mit der Entfernung. Die besten Kandidaten für die realistische Abbildung des Schattens sind also extrem schwere Schwarze Löcher in unserer Nähe. Aus diesem Grund ist das Zentrum unserer Milchstraße mit ihrer hellen Radioquelle, Sagittarius A*, ein ideales Objekt. Messungen der Eigenbewegung von Sternen im Galaktischen Zentrum (Eckart & Genzel 1996) haben deutlich gezeigt, dass es sich bei dieser Quelle wahrscheinlich um das zentrale Schwarze Loch der Milchstraße handelt, mit einer relativ genau bestimmten Masse von 3 Millionen mal der Masse der Sonne. Die Grösse des Schattens beträgt dann ungefähr den dritten Teil einer astronomischen Einheit und bei einer Entfernung von 8 kpc zum Galaktischen Zentrum entspricht dies einer Größe am Himmel von ~40 micro-Bogensekunden.

Auf den ersten Blick mag dies sehr klein erscheinen, aber tatsächlich haben Radioastronomen mit 3mm-VLBI inzwischen schon Bilder mit 50 micro-Bogensekunden Auflösung gemacht. Die dazu verwandte Technik nennt sich Very-Long-Baseline-Interferometry (VLBI; siehe Bild 3). Dabei werden weltweit Radioteleskope zusammengeschaltet deren Signale über einen Supercomputer - wie z. B. dem neuen MKIV-Korrelator in Bonn - korreliert werden und dann zu einem extrem hochauflösenden Bild von Radioquellen zusammengesetzt werden.

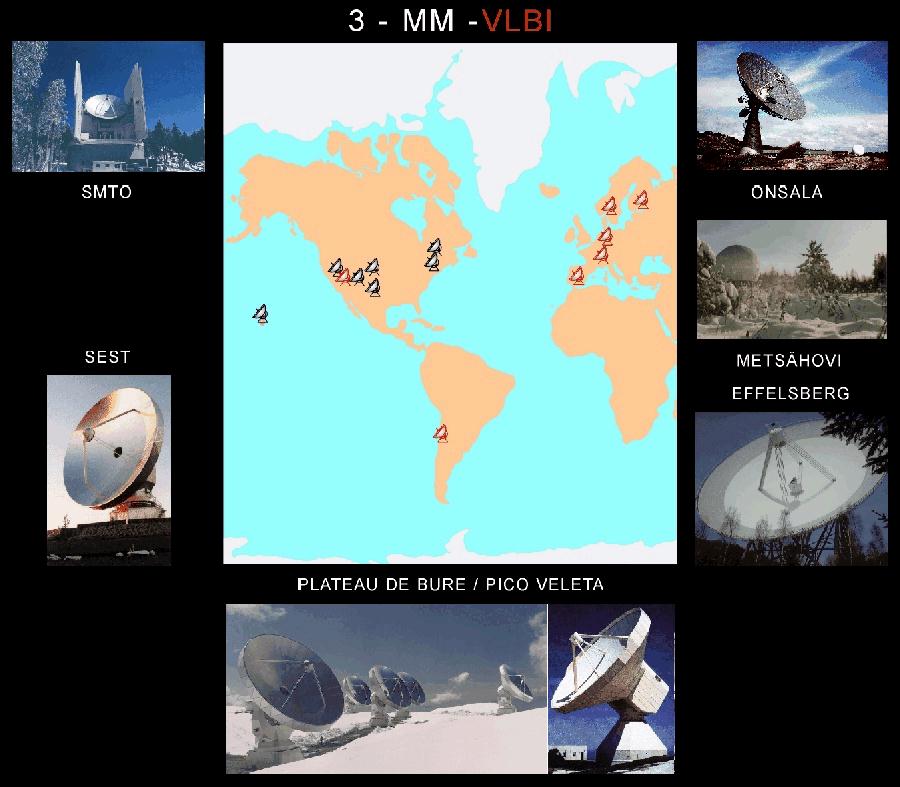
Bild 3: Millimeter VLBI. Das Bild zeigt eine Weltkarte mit der Position von amerikanischen (schwarz) und europäischen Teleskopen (rot), die bei 3mm-Wellenlänge beobachten und zu einem globalen Interferometer zusammengeschaltet werden können. Das zusammengeschaltete »Array« erreicht dann eine Auflösung die einem Radioteleskop mit dem Durchmesser der Erde entspricht.

Die höchsten Bildschärfen werden dabei bei den höchsten Frequenzen, also den kürzesten Wellenlängen, erreicht, d.h. inzwischen bei Wellenlängen um 3 mm (86 GHz). Interessanter Weise zeigen Beobachtungen von Sagittarius A*, dass tatsächlich die Emission bei dieser und kürzeren Wellenlängen aus der direkten Umgebung des Schwarzen Lochs kommen muss. Hinzu kommt, dass in einem Anfall seltener Freundlichkeit der Natur, die Emission von Sgr A* zu höheren Frequenzen heller und auch transparenter wird. Dies schafft geradezu ideale Verhältnisse, um den Schatten des Schwarzen Lochs wirklich abzubilden.

Zur Zeit scheitert dies aber noch daran, dass interstellares Material in der Milchstraße entlang unseres Sehstrahles das Bild bei Wellenlänge um 3mm (und länger) - wie ein Milchglas - verwäscht. Dieser Effekt verschwindet aber bei kürzeren Wellenlängen und höheren Frequenzen. Radioastronomen arbeiten daher z.Zt. daran VLBI auch bei 1.3 mm und vielleicht irgendwann auch 0.8 mm Wellenlänge erfolgreich durchzuführen. Der Bau neuer, großer Teleskope in diesem Frequenzbereich, wie z.B. ALMA, die Weiterentwicklung von Empfängern, und das Beherrschen atmosphärischer Korrekturen wird dabei sicher eine entscheidende Rolle spielen.

Bisher hat tatsächlich ein Experiment funktioniert, dass sich in diesen Bereich vorgewagt hat. Dabei wurde die Quelle Sgr A* mit 1.4 mm VLBI entdeckt (Krichbaum et al. 1998) und man stieß erstmalig in einen Bereich vor, der ganz dicht an dem vorhergesagten Schatten lag. Allerdings war die Qualität dieser ersten Daten noch so schlecht, dass man kein aussagekräftiges Bild rekonstruieren konnte. Weitere Verbesserungen werden viel Arbeit kosten und wertvolle Teleskopzeit verschlingen, aber die Aussichten sind motivierend. Gelingt es uns mit VLBI zu den höchsten Frequenzen vorzustoßen, dann werden wir mit größter Wahrscheinlichkeit den Schatten des Schwarzen Lochs und seines Ereignishorizonts sehen können - vorausgesetzt natürlich es existiert wirklich und Einstein hatte recht.

Referenzen:

Bardeen, J.M. 1973, in »Black Holes«, Eds. de Witt & de Witt (New York: Gordon & Breach), p. 215

Eckart, A., Genzel, R. 1996, Nature 383, 415

Falcke, H., Melia, F., Agol, E. 2000, ApJ 528, L13

Krichbaum, T. et al. 1998, A&A 335, L106

de Vries, A. 2000, Class. Qunatum. Grav. 17, 123

Autor:

Auf dem Hügel 69

53121 Bonn

hfalcke@mpifr-bonn.mpg.de

Tel.: 0225/525-217

Webseite mit englischer Dia-Show zu dem Thema:
http://www.mpifr-bonn.mpg.de/staff/hfalcke/bh